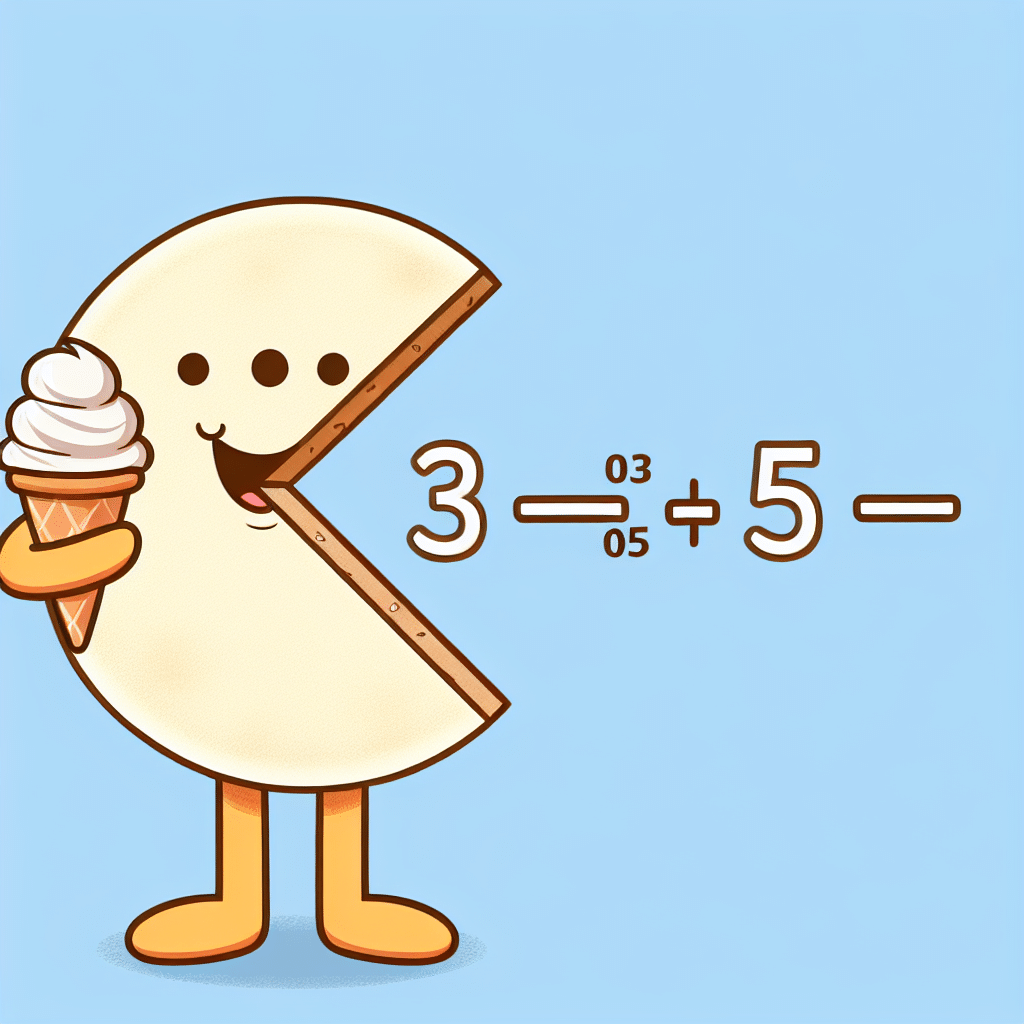The fraction for 0.6 is 3/5. To understand how to convert the decimal 0.6 into a fraction, let’s break it down. The number 0.6 can be expressed as 6 tenths, which is written as 6/10. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. When simplified, 6/10 becomes 3/5. Hence, 0.6 corresponds to the fraction 3/5. This understanding bridges the gap between decimals and fractions, providing a clear pathway for mathematical conversions.
Understanding Decimals and Fractions
Decimals and fractions are two ways of representing numbers that are not whole. While fractions display a relationship between two numbers (the numerator and the denominator), decimals represent values on a base-10 number system. Understanding how to convert between these forms is crucial for various mathematical applications.
Converting Decimals to Fractions
To convert a decimal like 0.6 into a fraction, you should follow a methodical approach:
- Identify the place value: The digit 6 in 0.6 is in the tenths place, meaning it represents 6 tenths.
- Write as a fraction: This gives us the fraction 6/10.
- Simplify the fraction: Divide both the numerator (6) and the denominator (10) by their greatest common divisor, which is 2. This simplifies to 3/5.
Thus, 0.6 = 6/10 = 3/5.
Exploring Equivalent Fractions
It’s vital to note that fractions can have equivalent forms. For instance, the fraction 3/5 can be represented in other ways by multiplying both the numerator and denominator by the same integer. Examples include:
- 6/10: Multiplying both 3 and 5 by 2.
- 9/15: Multiplying both 3 and 5 by 3.
- 12/20: Multiplying both 3 and 5 by 4.
All these fractions are equivalent to 0.6 when evaluated.
Practical Applications of Fractions and Decimals
Understanding the conversion between fractions and decimals aids in various real-world situations:
- Measurements: When working with recipes or construction, converting between decimal measurements and fractions is common practice.
- Financial calculations: Interest rates, discounts, and percentages frequently require decimal and fraction operations.
- Data interpretation: Statistics often display data in both formats, necessitating an understanding of their equivalences.
Decimal Representation of Fractions
Conversions work both ways. Recognizing how fractions can be written as decimals is just as crucial:
- Divide the numerator by the denominator: For instance, 3 ÷ 5 equals 0.6.
- Recognize repeating decimals: Some fractions lead to repeating decimals, such as 1/3 = 0.333… that can be rounded.
Common Mistakes and Misunderstandings
Many learners face confusion when converting between decimals and fractions. Here are a few common pitfalls:
- Ignoring place value: Failing to recognize the place value of decimals can result in inaccurate fraction representation.
- Not simplifying: Students often forget to simplify fractions, leading to unnecessary complexity.
- Overgeneralizing conversions: Assuming all decimals can be directly transformed into a fraction without consideration of their specific place value can lead to errors.
FAQs
What is the fraction for 0.75?
The fraction for 0.75 is 3/4, which can be derived from 75/100 when simplified.
How do you convert a repeating decimal to a fraction?
To convert a repeating decimal like 0.666… to a fraction, set it equal to a variable, multiply to shift the decimal point, and then subtract to isolate and simplify.
Are all decimals convertible to fractions?
Yes, every decimal can be expressed as a fraction, though some (like those with infinite repeating digits) may require specific methods to simplify accurately.
What is the importance of understanding fractions and decimals in daily life?
Understanding fractions and decimals is essential for managing finances, cooking, and conducting various measurements, making accurate calculations and comparisons in daily activities.
Final Thoughts
Recognizing how to convert 0.6 to the fraction 3/5 bridges the gap between decimal and fractional representations. Mastering this concept not only aids in academic pursuits but also enriches your practical life skills. As you continue to explore the world of numbers, understanding both forms will empower you in numerous endeavors, from simple problem-solving to complex calculations in finance and measurement.